Decadimento esponenziale ed emivita
Un semplice esperimento in cui si lanciano monete o dadi da gioco permette di capire perché il decadimento spontaneo di un sistema fuori dallo stato di equilibrio, ad esempio una certa dose di una sostanza radioattiva, avvenga sempre con legge esponenziale.
Con questo termine, si intende una variazione temporale tale che, in un dato intervallo di tempo, sempre lo stesso, la grandezza che va decadendo si riduce di un’eguale percentuale.
Facciamo un semplice esempio: si supponga di avere una grandezza che valga in partenza 100, e che un dato processo in corso abbia l’effetto di ridurla del 20% ogni secondo. Si otterrebbe la serie di numeri, intervallati appunto di un secondo, 100 – 80 – 64 – 51,2 – 40,96 – 32,768… e così via. Un processo esponenziale – come sono tutti quelli in cui un sistema perturbato torna spontaneamente verso le sue condizioni di equilibrio – termina dunque soltanto dopo un tempo infinito.
Quindi, poiché non è possibile attendere fino alla fine del processo per avere un’idea tangibile di quanto più o meno rapidamente esso si svolga, è conveniente definire un tempo di dimezzamento della grandezza iniziale, detto tempo di emivita o semplicemente emivita.
Nell’esempio precedente, l’emivita si trova rappresentando i valori numerici della grandezza studiata in funzione del tempo e cercando in quale istante essa assume il valore 50. Si trova subito che l’emivita è di 6,2 secondi.

La legge di decadimento esponenziale
Per i lettori che amano le formule, una legge di decadimento di tipo esponenziale si esprime tramite la relazione:
A(t)=A(0) exp(-t/τ)
dove A(t) è la grandezza in esame al tempo generico t e τ è un tempo caratteristico per il quale A(t) si riduce a un e-esimo del valore iniziale A(0). Poiché la base “e” della funzione esponenziale vale 2,7183, il tempo τ risulta circa 1,5 volte più lungo dell’emivita (più precisamente 1,4427 volte). Nell’esempio riportato in figura, varrebbe circa 9 secondi.
Quando avviene il decadimento esponenziale?
Per ricordare qualcuno dei tanti esempi di decadimento esponenziale nei processi fisici e organici, si può citare:
- in medicina, la diminuzione dell’efficacia di un medicinale, ad esempio un sonnifero, a partire dall’istante della sua assunzione;
- in elettricità, la diminuzione della carica accumulata su un conduttore quando viene scaricato a terra attraverso una resistenza;
- in fotoelettronica, il ritorno alla conducibilità elettrica normale di un semiconduttore che sia stato momentaneamente illuminato (ad esempio se usato come sensore di luce);
- in termodinamica, il ritorno alla temperatura ambiente di un corpo che sia stato riscaldato;
- in radiochimica, la diminuzione nel tempo dell’attività di un elemento radioattivo, per esempio il carbonio-14, utile nella datazione dei reperti archeologici.
Una facile verifica: capire il decadimento esponenziale usando le monete
Possiamo immaginare un semplice esperimento che permetta di simulare un modello di decadimento radioattivo e verificare che esso segue una legge esponenziale.
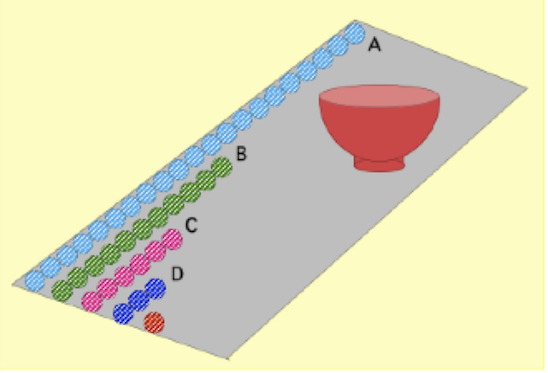
Procuriamoci 100 monete e poniamole in una ciotola. Dopo averle rovesciate sul tavolo, separiamo quelle che ci mostrano la “testa” da quelle che ci appaiono con la “croce” e allineiamole lungo il bordo del tavolo, formando una fila che chiameremo A. Rimettiamo nella ciotola le restanti monete (quelle con il risultato “croce”) e lanciamole ancora una volta, ottenendo, con le nuove monete “testa”, una seconda fila B. Si ripete il tutto, ottenendo via via delle file più corte; C, D…
Fatte salve ovvie fluttuazioni statistiche, mediamente a ogni lancio avremo raccolto e rimesso nella ciotola la metà delle monete rimaste disponibili. Quindi, se inizialmente erano 100, dopo ogni successivo lancio saranno circa 100/2, 100/4, 100/8, 100/16 e così via. Osserviamo che i numeri al denominatore si possono scrivere come potenze del due, 2, 22, 23, 24…, vale a dire che i numeri di monete disponibili per essere rilanciate si riducono sempre con una stessa modalità, proprio come si era detto nel definire un decadimento esponenziale.
Si può ripetere la prova con dei dadi, isolando quelli che escono con una data faccia, diciamo l’uno. In questo caso, essendo ogni volta la probabilità uno su sei, la serie sarà formata dalle potenze del 6.
Il decadimento radioattivo
E la radioattività? In che modo il nostro giochetto può rapportarsi al decadimento di un nucleo radioattivo? Il processo è perfettamente equivalente a quello del lancio di molti dadi.
Si abbia una sostanza costituita da N nuclei radioattivi, supponiamo l’uranio-238. Essi sono tutti eguali e la probabilità che, in un secondo, uno qualsiasi di essi decada in un elemento più stabile è identica a quella di ogni eventuale successivo secondo.
Se per le monete, a ogni lancio, una su due ha probabilità di uscire “testa”, supponiamo che per gli atomi, a ogni secondo, uno su N abbia la probabilità di cambiare natura.
Per certe sostanze la probabilità di un tale evento è estremamente piccola, ovvero N è grandissimo, e l’emivita può allungarsi a milioni di anni, com’è appunto il caso del decadimento dell’uranio-238 in piombo (il quale, per questa ragione, si presta a farci stimare l’età di un antico manufatto). All’altro estremo possiamo considerare il radon-217, che si dimezza in un solo millesimo di secondo, mentre il carbonio-14 ha un’emivita di 5600 anni, il che lo rende adatto alla datazione dei reperti archeologici (e allo smascheramento dei falsi nell’arte).

























